什么是聚类分析,Matlab代码教你一步步实现
在数据分析领域,我们常常需要从杂乱无章的数据中提取有意义的信息。聚类分析,如同一个数据分类师,它能够将数据样本按照相似性自动划分成不同的组别,也就是我们常说的“簇”。这些簇内部的样本彼此相似,而不同簇之间的样本差异显著。简单来说,聚类分析就像将一袋五颜六色的糖果按照颜色分成不同的堆,方便我们观察和研究每种颜色的糖果特点。
本文将从个人角度出发,深入浅出地介绍聚类分析的概念,并通过具体的Matlab代码示例,帮助读者一步步实现聚类分析。

1. 聚类分析的应用场景
聚类分析,作为一种无监督学习方法,广泛应用于各个领域,例如:
客户细分: 根据客户购买习惯、消费行为等特征将客户群体划分成不同的细分市场,以便针对性地进行营销和推广。
图像分割: 将图像中的像素点根据颜色、纹理等特征进行聚类,从而实现图像的自动分割和目标识别。
文本分析: 将文本数据根据主题、关键词等特征进行聚类,用于文本分类、主题提取和信息检索。
基因分析: 将基因序列根据相似性进行聚类,用于研究基因功能、进化关系等
2. 聚类分析的算法
聚类分析的算法种类繁多,每种算法都有其优缺点,适合处理不同的数据类型和以下介绍几种常用的聚类算法:
2.1 K-means聚类
K-means是最常见的聚类算法之一,它以简洁高效著称。算法的基本思想是:
随机选择K个样本点作为初始聚类中心。
然后,将每个样本点分配到距离其最近的聚类中心所在的簇。
接着,重新计算每个簇的中心点。
重复步骤2和3,直到聚类中心不再变化或达到最大迭代次数。
2.2 层次聚类
层次聚类算法根据样本之间的距离,逐步将样本合并或拆分,形成一个树状结构的层次结构。常见的层次聚类算法包括:
凝聚层次聚类: 从每个样本点作为一个独立的簇开始,逐步合并距离最近的两个簇,直到所有的样本点都被合并成一个簇。
分裂层次聚类: 从所有样本点在一个簇中开始,逐步将距离最远的样本点划分成不同的簇,直到每个样本点都成为一个独立的簇。
2.3 DBSCAN聚类
DBSCAN算法是一种基于密度的聚类算法,它能够识别形状不规则的簇。算法的基本思想是:
定义两个参数:半径ε和最小样本数MinPts。
然后,判断每个样本点是否是核心点,即其ε-邻域内包含至少MinPts个样本点。
根据核心点和非核心点之间的连接关系,形成不同的簇。
3. 聚类分析的关键步骤
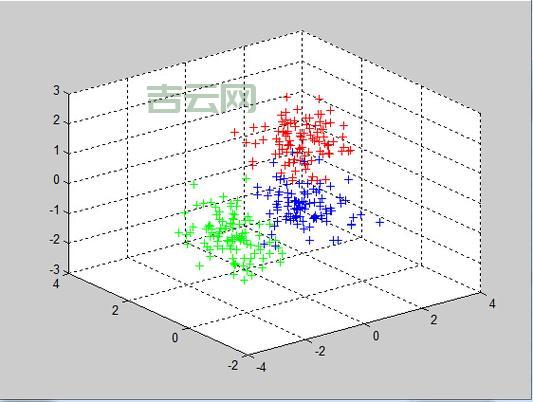
实现聚类分析通常需要经历以下几个步骤:
1. 数据预处理: 对数据进行清洗、标准化、降维等操作,以便提高聚类分析的效率和准确性。
2. 选择聚类算法: 根据数据特点和分析目的,选择合适的聚类算法。
3. 确定聚类参数: 根据数据特征和算法要求,设置聚类算法的参数,例如,K-means算法中的聚类中心数量K、DBSCAN算法中的半径ε和最小样本数MinPts。
4. 执行聚类分析: 使用选择的聚类算法对数据进行聚类分析,得到每个样本点的簇标签。
5. 评估聚类结果: 使用不同的指标评估聚类结果的质量,例如,轮廓系数、Calinski-Harabasz指标等。
4. Matlab代码实现聚类分析
以下代码演示了如何使用Matlab进行K-means聚类分析:
matlab
% 加载数据
data = load('data.mat');
X = data.X;
% 选择聚类中心数量
K = 3;
% 执行K-means聚类
[idx, C] = kmeans(X, K);
% 可视化聚类结果
figure;
hold on;
for i = 1:K
plot(X(idx == i, 1), X(idx == i, 2), 'o', 'MarkerFaceColor', rand(1, 3));
end
plot(C(:, 1), C(:, 2), 'kx', 'MarkerSize', 12, 'LineWidth', 2);
title('K-means聚类结果');
xlabel('特征1');
ylabel('特征2');
hold off;
代码解释:
加载包含数据的mat文件,将数据存储到变量X中。
然后,设置聚类中心数量K为3。
接着,调用kmeans函数进行K-means聚类,并将结果存储到变量idx和C中,其中idx表示每个样本点的簇标签,C表示每个簇的中心点。
使用plot函数将聚类结果可视化,不同颜色表示不同的簇,黑色十字表示聚类中心点。
5. 如何选择合适的聚类算法
选择合适的聚类算法需要根据数据的特点和分析目的进行综合考虑,以下是一些建议:
数据类型: 如果数据是连续数值型数据,可以选择K-means、层次聚类等算法;如果数据是离散型数据,可以选择K-modes等算法。
数据分布: 如果数据呈球形分布,可以选择K-means算法;如果数据呈非球形分布或存在噪声点,可以选择DBSCAN算法。
簇形状: 如果簇的形状是规则的,可以选择K-means算法;如果簇的形状是不规则的,可以选择DBSCAN算法。
效率要求: 如果需要高效的算法,可以选择K-means算法;如果需要更精确的算法,可以选择层次聚类算法。
关于聚类分析的思考
聚类分析可以帮助我们从数据中挖掘隐藏的模式,并根据这些模式对数据进行分类和解释。但聚类分析的结果并不一定是唯一的,不同的聚类算法、不同的参数设置,都可能导致不同的聚类结果。在进行聚类分析时,我们需要根据实际情况选择合适的算法和参数,并结合其他分析手段对聚类结果进行评估和解释。
您在实际项目中遇到过哪些聚类分析的应用场景呢?欢迎分享您的经验和见解!

